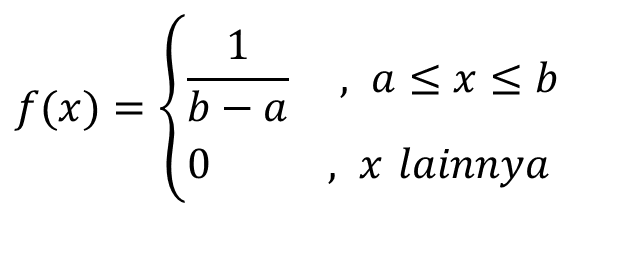Pengin Belajar Seputar IT

Fungsi Peluang (pmf) Definisi : Jika X adalah p.a.d ., suatu nilai P *(xi )= P( X = xi ) dimana xi adalah outcome dalam R*  utk i =1, 2, 3, …, n.  pX(xi) harus memenuhi: Fungsi pX(x) disebut fungsi massa peluang fmp ) /  probability mass function (pmf) FUNGSI DISTRIBUSI KUMULATIF (CDF) Fungsi distribusi kumulatif (cdf) FX(x) daripeubah acak X didefinisikan sebagai peluang dari kejadian {X<=x} atau P (X<=x) Sifat sifat cdf : Mean (rataan) Lambang E disebut operator Ekspektasi Beberapa istilah ekspektasi : rataan , nilai harapan matematika Sifat-sifat mean : 1.E(k) = k 2.E( kX ) = k E(X) ; dengan k adalah konstanta 3.E(a + bX ) = a + b E(X) ; ; dengan a dan b adalah konstanta Variansi sifat-sidat variansi : 1.Var(k) = 0 2.Var( kX ) = k 2 Var(X) ; dengan k adalah konstanta 3.Var(a + bX ) = b 2 Var(X) ; dengan a dan b adalah konstanta

     Dalam proses stokhastik, distribusi uniform ini banyak terkait, bahkan kontribusinya dalam engineering sangat berperan.  Peubah acak uniform muncul dalam situasi dimana semua nilai dalam selang/interval tertentu mempunyai peluang yang sama untuk muncul. Fungsi Padat Peluang Definisi : Fungsi padat peluang untuk peubah acak X yang berdistribusi uniform pada interval (a,b), adalah :  Rataan dan Variansi Contoh Soal Diketahui variabel acak X berdistribusi Uniform dalam interval (2,7), hitunglah :      a . fungsi padat peluang      b. rataan dan variansi      c. p(x>=4) pembahasan soal :  https://www.youtube.com/watch?v=R4kAzPGTO8g